从关系代数到 SQL
关系模型与关系代数是关系型数据库系统的基础,SQL 是用户与数据库系统交互的媒介。本文简要介绍关系模型与关系代数的基本内容,从展示关系代数在 SQL 中的对应语句。
1. 关系模型
关系模型是对数据库系统的抽象,其用 “关系” 来表示数据库,而隐藏数据在数据库系统内部是如何组织的。关系模型的核心原则是:
- 以简单的数据结构(关系)存储数据库。
- 物理存储结构由 DBMS 实现决定。
- 通过高级语言访问数据,DBMS 负责找到最好的执行策略。
关系模型具有几个关键概念:
- 关系(relation):关系是包含表示实体的属性关系的无序集合。
- 元组(tuple):元组是关系中的一组属性值。
2. 关系代数
关系代数是用于操作关系模型的工具,以在数据库中进行查询等操作。关系代数的每个操作符接受一个或多个关系作为其输入,并输出一个新的关系。关系代数运算符根据输入的关系数量可分为单目运算符和双目运算符。最常用的操作有:
- 选择(Select):\(\sigma\)
- 投影(Projection):\(\Pi\)
- 并集(Union):\(\cup\)
- 交集(Intersection):\(\cap\)
- 差集(Difference):\(-\)
- 笛卡尔积(Product):\(\times\)
- 连接(Join):\(\bowtie\)
- ……
2.1 选择
含义:从关系中选择满足选择谓词的元组。谓词用来充当过滤器,仅保留满足谓词条件的元组。可以使用合取/析取合并多个谓词。
语法:\(\sigma_{predicate}(\text{R})\)
例子:\(\sigma_{ {\text{a}\_\text{id}=\text{'a2 '}} \wedge {\text{ b}\_\text{id} > \text{102}}}(\text{R})\)
SQL:
1 | |
2.2 投影
含义:用只包含指定属性的元组生成关系。可用于重新排列属性顺序和操作属性的值。
语法:\(\Pi_{ \text{A1},\text{A2},...,\text{An} }(\text{R})\)
例子:\(\Pi_{ \text{b}\_\text{id-100},\text{a}\_\text{id} }( \sigma_{ \text{a}\_\text{id}=\text{'a2'} }(\text{R}) )\)
SQL:
1 | |
2.3 并集
含义:生成一个关系,其中包含只出现在一个或两个输入关系中的所有元组。
语法:\(\text{R} \cup \text{S}\)
SQL:
1 | |
2.4 交集
含义:生成一个关系,该关系只包含出现在两个输入关系中的元组。
语法:\(\text{R} \cap \text{S}\)
SQL:
1 | |
2.5 差集
含义:生成一个关系,其中只包含第一个输入关系中出现的元组,而不包含第二个输入关系中出现的元组。
语法:\(\text{R} - \text{S}\)
SQL:
1 | |
2.6 笛卡尔积
含义:生成包含来自输入关系的元组的所有可能组合的关系。
语法:\(\text{R} \times \text{S}\)
SQL:
1 | |
2.7 连接
含义:生成一个包含元组的关系,该元组是两个具有一个或多个属性的共同值元组(每个输入关系一个)的组合。
语法:\(\text{R} \bowtie \text{S}\)
SQL:
1 | |
连接操作还可以附加谓词,相当于先做笛卡尔积再进行选择操作,见 《Database System Concepts》一书解释:

这种形式相当于以下 SQL:
1 | |
2.8 赋值
含义:提供一种工具,更容易地表达复杂查询。
符号:\(\leftarrow\)
例子:
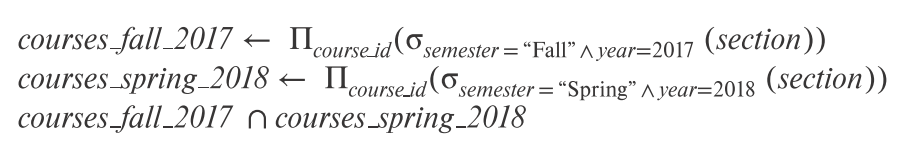
2.9 重命名
含义:用于给关系代数计算中间结果取名。
符号:\(\rho\)
语法:\(\rho_{\text{x} }(\text{E})\) 或 \(\rho_{\text{x} ( \text{A1},\text{A2},...,\text{An} ) }(\text{E})\)
SQL:
1 | |
2.10 聚合
含义:计算 AVG、MAX、MIN、SUM、COUNT 值
符号:\(\gamma\)
例子:\(_\text{A2} \gamma_{ \textbf{average}\text{(A1)}} (R)\) ,表示在关系 R 上,在 A2 属性上分组,计算 A1 属性的平均值。
SQL:
1 | |
更复杂的例子:

参考: